Closed
Nach über einem Jahr ohne neuen Post ist es an der Zeit, den KosRef Blog offiziell zu schließen. Leider habe ich nicht mehr die Zeit und auch nicht mehr die Motivation, hier neues zu schreiben. Deshalb dieser letzte "Closed" Artikel, um diesen Blog (mehr oder weniger) sauber zu schließen. Die alten Artikel bleiben aber natürlich online, da sie meiner Meinung nach ein schönes Zeugnis aus alten Zeiten sind.
Geschrieben am 01.05.2009 von Stefan | Kommentar hinzufügen (0)
Geschicktes Rechnen mit Längenmaßen
Viele Schüler haben Schwierigkeiten bei der Umrechnung von Längen- und Flächenmaßen. Ich kenne das auch noch von früher: Man wusste nie, durch was denn bei der Umrechnung von cm² in m² geteilt werden muss. Bzw. man hat es nur so gelernt: Quadratzentimeter in Meter, geteilt durch 10000. Dabei ist dieses sture Pauken ohne die Zusammenhänge zu verstehen absolut uneffektiv, denn sobald sich nur die Größenordnungen ändern, steht man wieder im Wald.
Wenn man sich aber einmal mit diesen Maßen richtig beschäftigt, kann man eine Technik entdecken, welche nicht nur universell funktioniert, sondern auch einfach nur elegant ist.
Zuerst einmal schauen wir uns die Abkürzung cm genauer an. Für was stehen denn die beiden Buchstaben? Die Einheit Meter wird immer durch das m definiert. Der Buchstabe davor ist eigentlich eine Zahl und gibt eine Größenordnung an. Verbunden sind die beiden durch einen Malpunkt. c steht hierbei für Zenti und ist ein Vorsatz für Maßeinheiten. Damit vermeidet man lange Zahlen, indem man die Nullen salopp gesagt in die Abkürzung packt. Das c könnte man also auch als 0,01, 1/100 oder am Geschicktesten als 10^(-2) schreiben.
An dieser Stelle hat man nun schon was ganz Wesentliches gelernt. Um Längenmaße egal welcher Gestalt (z.b. cm oder km) in Meter umzurechnen reicht es, einfach diesen Vorsatz als Zahl zu schreiben und bei Bedarf eben ein wenig zu rechnen. Aus 5000 cm ergeben sich so 5000 * 0,01 m , was genau 50 Meter entspricht. Natürlich muss man dazu die Vorsätze und ihre Wertigkeit kennen. In der Wikipedia gibt es eine ausführliche Liste dazu. Ausdrucken, an die Wand neben dem Schreibtisch hängen und nach ein paar Mal rechnen hat man die drauf.
Aber wie funktioniert die andere Richtung? Wie kommt man von Meter auf Millimeter? Klar, man könnte erst mit 100 malnehmen(m --> cm) und dann noch mit 10. Aber wir wollen es gleich richtig lernen. Millimeter (mm) ist ja nichts anderes als 0,001 * m. Milli steht für Tausendstel. Wie bekommt man nun in den Ausdruck 1 m diesen Faktor Milli rein? Ganz einfach: Wir fügen eine nahrhafte Eins ein. In jedes Produkt dürfen ja beliebig viele 1er hineingeschrieben werden. 5*6 ist genau dasselbe wie 1*5*1*6*1. Damit die eins "nahrhaft" wird, was soviel bedeutet wie nutzbar, kann man sie auch als Bruch schreiben, mit identischem Zähler und Nenner. Das sieht dann so aus:
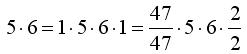
Alles genau dasselbe, oder? In diesem Fall ein blödes Beispiel, aber für unser Maßeinheitenproblem macht das verdammt viel Sinn:
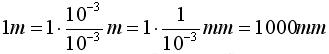
Wir fügen die nahrhafte Eins ein, wandeln das 10^(-3) im Zähler in Milli um und rechnen die restlichen Zahlen aus. Natürlich muss man sich ab dieser Stelle mit den Potenzgesetzen auskennen. Wer noch nicht soweit ist fügt eben statt 10^(-3) 0,001 im Zähler und Nenner ein, das ist genau dasselbe.
Das ist eigentlich schon der ganze Trick. Durch geschicktes Einfügen von nahrhaften Einsen kann man Längeneinheiten so umformen, wie man es gerne möchte. Um von Millimeter zu Kilometer zu kommen muss eben mit 10^6 / 10^6 erweitert werden. So bildet sich im Zähler das Kilo und im Nenner bleibt ein 10^6. Euer Lehrer würde hier sagen: "Durch eine Million teilen". Daher kommen nämlich auch diese ominösen Faktoren zum Umrechnen, welche man sonst immer auswendig lernen musste.
Exakt gleich funktioniert auch das Umrechnen von Flächen- und Volumenmaßen. Hier gibt es nur einen kleinen Fallstrick, eine ungenaue Schreibweise, welche oft für Verwirrung sorgt: cm² steht ja für Quadratzentimeter. Das Quadrat bezieht sich an dieser Stelle aber nicht nur auf die Meter, sondern auch auf das Zenti. Korrekterweise müsste man also (cm)² schreiben, was identisch zu c² * m² ist. Nun kann man wieder wie oben verfahren: Nahrhafte 1 einfügen, um den gewünschten Vorfaktor zu bilden, restliche Zahlenwerte ausrechnen. Aber Achtung: Auch hier muss das Quadrat wieder berücksichtigt werden. Um (km)² zu bilden, muss ein Faktor 10^6 im Term geschaffen werden.
Ein Beispiel hierzu:
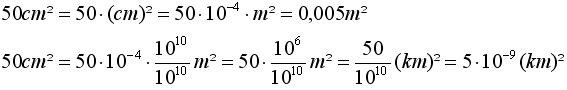
Das ist alles. Nun seid ihr bestens gerüstet für alle Arten von Längen-, Flächen- und Volumenumrechnungen.
Geschrieben am 03.06.2007 von Stefan | Kommentar hinzufügen (0)
400000
Mir ist gerade aufgefallen, dass diese Woche mal wieder ein Besuchermilestone erreicht wurde. Über 400.000 Besucher haben seit September 2000 KosRef besucht. Interessant sind wie immer die Wachstumsraten: Die ersten 200.000 Besucher kamen von September '00 bis März 2006, also mehr als 5 Jahre. Die nächsten 200.000 dauerten nur noch knapp 14 Monate. Ich bin gespannt wie sich dieses Wachstum in den kommenden Monaten entwickeln wird, wobei die Sommermonate natürlich nicht repräsentativ sind.
Geschrieben am 27.04.2007 von Stefan | Kommentar hinzufügen (0)
Alte Prognose
Am 20.März schrieb ich über die aktuellen KosRef Besucherzahlen. Anlass war der 200.000ste Besucher auf der Seite. Damals stellte ich die kühne Prognose auf, dass wohl im Oktober Nr. 300.000 zu erwarten sei. Leider hat es nicht ganz gereicht: Der Sommer war wohl doch zu ruhig. Klar, wer sucht in den Sommerferien nach Referaten? Dafür waren aber die letzten beiden Monate mehr als ein Ausgleich, mit regelmäßig über 1000 uniqe Visits pro Tag. Gibt in der Summe dann 300000 Besucher am Mittwoch, den 6.Dezember 06. Also nur knapp verschätzt..
Neue Prognose? Ab heute 110 Tage, also ungefähr Mitte/Ende März. Wahrscheinlich sogar im gleichen Zeitraum wie dieses Jahr bei der 200000er Marke.
Geschrieben am 08.12.2006 von Stefan | Kommentar hinzufügen (0)
Rechnen wie früher
Wenn man sich auf eine Klausur ohne Taschenrechner vorbereitet kommt man immer wieder in Situationen, die mit Rechner einfach trivial wären, ohne Rechner aber kurz innehalten lassen. Dazu gehört z.b. alles was mit dem Arctan zu tun hat. Ich kenn den Sinus und Kosinus auswendig, den Tangens einigermaßen, aber beim Arctan hört es einfach (noch...) auf. Ebenfalls gar nicht so leicht: Zwei Brüche vergleichen und entscheiden, welcher denn nun größer ist. Bei 1/3 und 1/4 sollte es auf einen Blick zu sehen sein, was ist aber mit 4/7 und 10/17? Wie kann man schnell ohne Taschenrechner bestimmen, welcher der beiden Brüche größer ist?
Nach bisschen überlegen ist mir eine ganz gute Möglichkeit in den Sinn gekommen. Man stellt einfach eine Ungleichung auf und behauptet damit z.b., a > b. Diese Gleichung formt man dann um, bis eine eindeutige Aussage dasteht. War die ursprüngliche Annahme richtig, steht was Wahres da. War die ursprüngliche Annahme falsch, dann gibt es was falsches.
Beispiel gefällig? Welcher Bruch ist größer, 4/7 oder 10/17? Ich vermute mal 10/17. Also heißt die Ungleichung:
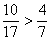
Die wird jetzt einfach umgeformt. Mit 17 und 7 durchmultipliziert ergibt
10 * 7 > 4 * 17
Und das ist einfach
70 > 68
Diesen Ausdruck können wir auswerten, 70 ist größer als 68, die Ungleichung ist wahr. Damit war die ursprüngliche Annahme ebenfalls wahr. Hätten wir in der Ungleichung zu Beginn die andere Annahme getroffen, dann würde die Rechnung am Schluss "falsch" ergeben. Das hilft uns genau so weiter. Diese recht elegante Rechnung hilft also schnell beim Vergleichen von Brüchen weiter.
Ach ja:
10/17 = 0,58...
4/7 = 0,57...
Geschrieben am 08.12.2006 von Stefan | Kommentar hinzufügen (0)
Auszeit
Ankündigung in eigener Sache: Kommenden Dienstag ab 16:00 Uhr wird der Blog für einige Zeit nicht erreichbar sein. Mein Provider macht ein Serverupdate, komplett mit Aktualisierung des Betriebssystems und der Programme. Im Optimalfall wurden mir 6 Stunden downtime versprochen, also bin ich guter Dinge dass bis spätestens Mittwoch morgen alles wieder läuft.
Geschrieben am 21.10.2006 von Stefan | Kommentar hinzufügen (0)
Neues Futter für Studenten
Für Studenten war das Angebot an Referaten und Downloads auf KosRef bisher recht dünn. Die meisten Arbeiten sind für die Mittel- und Oberstufe gedacht; mit denen kann ein Unistudent natürlich nichts anfangen. Auch meine schönen Physik - Ausarbeitungen aus dem LK entlocken einem Physikstudenten wohl nur ein müdes Lächeln.
Unsere neue Rubrik "Studienliteratur" dagegen richtet sich speziell an Studenten an Unis und FHs. In Zusammenarbeit mit studentensupport.de bieten wir euch nun hochwertige Lehr- und Übungsbücher zum kostenlosen Download! Die Dateien liegen im PDF - Format vor und können somit auf allen Systemen gelesen und gedruckt werden. Geboten werden momentan Bücher für Wirtschaftsstudenten, also aus dem Bereich BWL, VWL und Mathe. In Zukunft sollen aber auch angehende Ingenieure und Informatiker versorgt werden.
Der Verlag hinter studentensupport.de stellt die Bücher natürlich nicht ganz ohne Eigennutz frei ins Netz. Mit Werbung auf jeder dritten Seite muss man leben. Dafür stimmt die Qualität der Bücher, sie stammen aus den Federn von Uniprofessoren. Ein Download lohnt sich also in jeden Fall.
Geschrieben am 01.06.2006 von Stefan | Kommentar hinzufügen (0)
Giga.de Homepage Award
KosRef ist für den Giga Homepage Award 2006 nominiert. Heute hab ich eine E-Mail bekommen, in der die Aufnahme ins Ranking bestätigt wurde. Ich hoffe natürlich, dass ihr KosRef alle fleißig eure Stimme gebt! :)
Zu finden ist der Vote direkt unter http://www.giga.de/aktionen/homepageaward/index.php?use=votingkat&kat=14
Geschrieben am 24.04.2006 von Stefan | Kommentar hinzufügen (0)
Neue Startseite
Wie man unschwer erkennen kann hab ich die Startseite von KosRef überarbeitet. Der Blog ist ab sofort nur noch auf der Unterseite ./blog.html zu finden. Warum das? Ich weiß natürlich, dass der Blog damit die ganze "Laufleserschaft" verloren hat, welche auf der Suche nach Referaten zumindest die Überschriften der Einträge mitgenommen hat. Mit dem Rückzug ins "Hinterzimmer" lesen jetzt nur noch jene die Artikel, welche über den RSS-Feed dabei sind oder einzelne Artikel via Google gefunden haben. Aber ganz ehrlich: Mir ist ein interessiertes Publikum lieber als 1000 flüchtige Leser, die den Blog 10 Sekunden später sowieso wieder vergessen haben.
Mit der neuen Startseite verfolge ich noch ein anderes Ziel. KosRef soll wieder mehr auf das reine Schüler- und Referateportal fixiert werden. Ein Blog auf der Startseite, welcher bunt gemischt mal über Politik oder das Web2.0 schreibt, fördert das nicht unbedingt. Mit einer themenfixierten Startseite aber können sich Google und Co. besser darauf einschießen.
Geschrieben am 12.04.2006 von Stefan | Kommentar hinzufügen (0)
200.000+
Die erste Million ist immer am schwersten. Wenn man die aber mal hat, gehts immer schneller aufwärts. Das gilt nicht nur für Geld, sondern auch für Besucherzahlen auf einer Homepage. Für die ersten 100.000 hat KosRef noch über vier Jahre gebraucht, im Dezember 2004 war es soweit. Die zweiten 100.000 sind nun schon innerhalb von 15 Monaten auf die Seite gekommen. Macht zusammen 200.XXX Besucher, zu sehen seit heute morgen im Counter im Footer der Seite :)
Es werden noch Wetten angenommen, wann wir die 300.000er Marke durchbrechen. Mit den aktuellen Zahlen im Hinterkopf peile ich mal ungefähr... Oktober 2006?!? an. Bitte erinnert mich an diese kühne Prognose, wenns soweit ist.
Geschrieben am 20.03.2006 von Stefan | Kommentar hinzufügen (0)

