Lösen von inhomogenen linearen Gleichungssystemen

Ein Gleichungssystem ist in der Form A*x = b gegeben. A ist bekannt, b ist bekannt. Für welche Werte x ist das Gleichungssystem wahr?

Sei A eine (m x n) Matrix mit m = 5, n = 7

1. Im ersten Schritt wird die Matrix A mit elementaren Zeilenumformungen auf Zeilenstufenform gebracht. Der Vektor b wird ebenfalls mit umgeformt.
Wikipedia: http://de.wikipedia.org/wiki/Gau%C3%9Fsches_Eliminationsverfahren

Nach den Zeilenumformungen hat die Matrix folgende Gestalt:

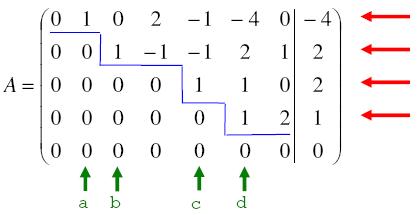
Was sagt uns die Zeilenstufenform?

• Die Matrix hat 4 linear unabhängige Zeilen
• Die Matrix hat 4 linear unabhängige Spalten a,b,c,d
• Der Rang der Matrix ist 4. rg(A) = 4
• Das LGS ist lösbar, da gilt: rg(A) = rg(A;b)
• Die Dimension des Lösungsraumes ist 3. dimL(A;0) = n – rg(A) = 7 – 4 = 3 .

Daraus folgt: Es gibt mehrere Lösungen für das LGS.

Notiz:
Wäre dimL(A;0) = 0 --> LGS ist eindeutig lösbar, es gibt nur eine Lösung
Wäre m = rg(A) -- >LGS ist universell lösbar, d.h. für beliebige b’s lösbar.

2. Nun berechnen wir eine spezielle Lösung des LGS. Eine spezielle Lösung ergibt sich aus einem eigenen kleinen Gleichungssystem der vier linear unabhängigen Spalten mit dem Vektor b.

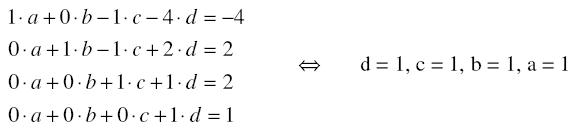
Eine spezielle Lösung des LGS ist also der Vektor x mit

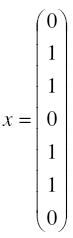
3. Nun berechnen wir die allgemeine Lösung des LGS. Diese setzt sich zusammen aus der speziellen Lösung und der Lösung für das Gleichungssystem A*x = 0. Wir müssen dieses nun also auch lösen.

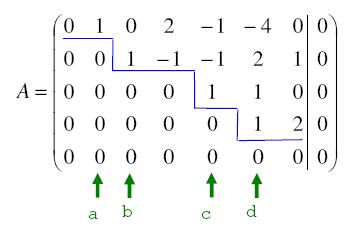
Von vorhin wissen wir noch: dimL(A;0)= 3
--> Die Basis unseres Lösungsraumes L(A;0) hat die Dimension 3. Wir müssen also drei Vektoren finden, welche die Basis des Lösungsraumes bilden.

v1 = (1,0,0,0,0,0,0)
v1 ist ein Vektor der Basis. Multipliziert man mit diesem Vektor alle Zeilen der Matrix durch, kommt immer 0 heraus. Und genau das suchen wir doch: Drei Vektoren, welche das Gleichungssystem L(A;0) lösen und dadurch eine Basis des Löungsraumes von L(A;0) bilden.

v4 = (0,n, n,1,0,0,0)
v4 ist auch einer der gesuchten Vektoren. Allerdings fehlen uns noch zwei Stellen, welche wir mit dem folgenden LGS berechnen können. Wichtig: Vorherige linear abhängige Spalten, welche bei der Berechnung auf 1 gesetzt waren, sind nun 0.

--> Mit b = 0 und a = -2 lautet der gesuchte Vektor v4
v4 = (0,-2, 1,1,0,0,0)

v7 = (0,n, n,0, n,n,1)
Dieses Mal fehlen 4 Stellen, welche wieder mit einem LGS berechnet werden.

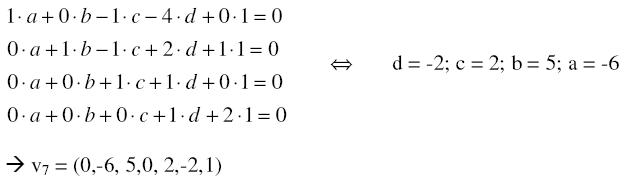
Nun haben wir v1, v4 und v7 berechnet. Diese bilden nun eine Basis des dreidimensionalen Lösungsraumes von L(A;0).

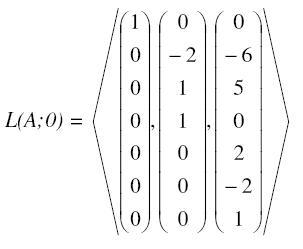
Bemerkung: Die drei Vektoren sind natürlich linear unabhängig.

Die spezielle Lösung und die allgemeine Lösung bilden zusammen die Lösung des inhomogenen linearen Gleichungssystems:

X = x + ß1 * v1 + ß4 * v4 + ß7 * v7

Die ßi sind hierbei nur Skalare. Aus der Lösung können wir folgern:
Für beliebige ß1, ß4, ß7 ergibt die Linearkombination einen Vektor X, welcher das inhomogene LGS löst.